Per Azure Databricks documentation, "Delta Lake is an open source storage layer that brings reliability to data lakes. Delta Lake provides ACID transactions, scalable metadata handling, and unifies streaming and batch data processing. Delta Lake runs on top of your existing data lake and is fully compatible with Apache Spark APIs." Basically, Delta gives us the ability to create tables using Azure Databricks, with many of the fantastic features commonly found in proprietary database technologies such as:
- ACID Transactions: Delta guarantees that all readers and writers are working with consistent data, even in highly transactional environments.
- Scalable Metadata Handling: Delta improves on one of the most common issues with Data Lakes by managing metadata for billions of records at scale.
- Schema Enforcement: Delta can strongly enforce schema requirements for Delta-enabled tables.
- Time Travel: Delta can store historical data and automatically query relevant data for any requested time period.
In a future post, we'll take a look at each of these features, comparing Delta tables to traditional external hive tables. Before that, we need a Data Frame and a couple tables to work with. For these posts, we'll be working with Python and SQL because they are approachable and easy to code.
<CODE START>
df = sqlContext.read \
.option("inferSchema", "true") \
.csv("/databricks-datasets/adult/adult.data").toDF( \
"age" \
,"workclass" \
,"fnlwgt" \
,"education" \
,"educationnum" \
,"maritalstatus" \
,"occupation" \
,"relationship" \
,"race" \
,"sex" \
,"capitalgain" \
,"capitalloss" \
,"hoursperweek" \
,"nativecountry" \
,"income" \
)
df_adult.show(2)
<CODE END>
Next, let's create an external Hive table and a Delta table.
<CODE START>
 |
| df |
<CODE START>
df = sqlContext.read \
.option("inferSchema", "true") \
.csv("/databricks-datasets/adult/adult.data").toDF( \
"age" \
,"workclass" \
,"fnlwgt" \
,"education" \
,"educationnum" \
,"maritalstatus" \
,"occupation" \
,"relationship" \
,"race" \
,"sex" \
,"capitalgain" \
,"capitalloss" \
,"hoursperweek" \
,"nativecountry" \
,"income" \
)
df_adult.show(2)
<CODE END>
Next, let's create an external Hive table and a Delta table.
 |
| Save Hive Data |
<CODE START>
df.write.format("parquet").mode("overwrite").save("/mnt/delta/hive/")
<CODE END>
 |
| Create Hive Table |
<CODE START>
%sql
CREATE EXTERNAL TABLE hive (
age INT
,workclass STRING
,fnlwgt DOUBLE
,education STRING
,educationnum DOUBLE
,maritalstatus STRING
,occupation STRING
,relationship STRING
,race STRING
,sex STRING
,capitalgain DOUBLE
,capitalloss DOUBLE
,hoursperweek DOUBLE
,nativecountry STRING
,income STRING
)
LOCATION '/mnt/delta/hive/'
STORED AS PARQUET
<CODE END>
 |
| Query Hive Table |
<CODE START>
%sql
SELECT COUNT(1) FROM hive
<CODE END>
There's nothing new here. For a more in-depth view of Hive tables, check out our earlier post on the topic. Let's take a look at the Delta table now.
 |
| Save Delta Data |
<CODE START>
df.write.format("delta").mode("overwrite").save("/mnt/delta/delta/")
<CODE END>
 |
| Create Delta Table |
<CODE START>
%sql
CREATE TABLE delta
USING DELTA
LOCATION '/mnt/delta/delta/'
<CODE END>
 |
| Query Delta Table |
<CODE START>
%sql
SELECT COUNT(1) FROM delta
<CODE END>
 |
| Hive Files |
 |
| Delta Files |
The main difference we see is that the Delta files maintain a log, while the Hive files do not. This is one of the major features that allows Delta tables to function more like mature database tables. It also enables the Time Travel feature. Let's use ParquetViewer to take a peak at these files.
 |
| Hive Parquet File |
 |
| Delta Parquet File |
Excusing the small picture size, these files are identical. Let's see what happens if we duplicate the data in the tables.
 |
| Insert Hive Data |
<CODE START>
%sql
INSERT INTO hive
SELECT * FROM hive
<CODE END>
<CODE START>
%sql
SELECT COUNT(1) FROM hive
<CODE END>
 |
| Insert Delta Data |
<CODE START>
%sql
INSERT INTO delta
SELECT * FROM delta
<CODE END>
<CODE START>
%sql
SELECT COUNT(1) FROM delta
<CODE END>
We see that the INSERT commands ran perfectly for the Hive and Delta tables. Let's see what the storage looks like now.
 |
| Duplicated Hive Files |
 |
| Duplicated Delta Files |
 |
| Duplicated Delta Logs |
 |
| Hive _committed_ |
Despite not having a file extension, the Hive "_committed_" file is json formatted and only displays the files that were added and removed from the directory. The other "_committed" file looks identical with a different file name in the "added" section. Let's move on to the Delta log files.
The "00000000000000000000.json" file was written when the table was originally created and populated. It contains multiple sections, the first of which is the "commitInfo" section with basic information about the action that was taken.
The "protocol" section appears to contain information about who can read or write either the table files or the log files. Perhaps this will make more sense as we see more examples.
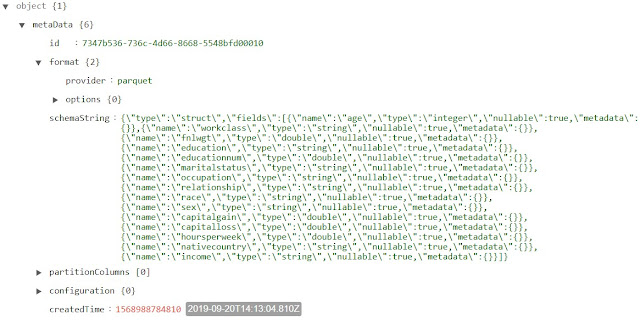
The "metadata" section contains all of the format and schema information about the table. Interestingly, the "schemaString" attribute is an escaped JSON string. Let's manually deconstruct it to see its format.
As expected, the "schemaString" attribute has a ton of information about each field, stored in an array named "fields".
Moving on to the file section of the first file, we see that the "add" section has information on the file that was added. This includes some basic stats about the data. Let's unwrap this field as well.
The "stats" section contains the total number of records in the file, as well as the minimum, maximum and number of nulls in each field. Now, let's take a look at the "00000000000000000001.json" file.
Since this file was created by the duplication operation, it has its own "commitInfo" section that looks very similar to the previous one. The major difference is that the "operationParameters.mode" attribute is Append instead of Overwrite.
The "add" section looks virtually identical to the one we saw previously. This makes sense because we did an exact duplication of the data in the table.
So, we've seen what happens when we add records to the table. But, what happens when update or delete records, or even drop the entire table? These questions will have to wait for later posts. We hope that this post enlightened you a little bit to the purpose and structure of Azure Databricks Delta. Stay tuned for the next post where we'll dig a little deeper into the inner workings. Thanks for reading. We hope you found this informative.
Brad Llewellyn
Service Engineer - FastTrack for Azure
Microsoft
@BreakingBI
www.linkedin.com/in/bradllewellyn
llewellyn.wb@gmail.com
 |
| Duplicated Delta Logs commitInfo |
 |
| Duplicated Delta Logs protocol |
 |
| Duplicated Delta Logs metadata |
 |
| Duplicated Delta Logs schemaString |
 |
| Duplicated Delta Logs add |
 |
| Duplicated Delta Logs stats |
 |
| Duplicated Delta Logs commitInfo 2 |
 |
| Duplicated Delta Logs add 2 |
So, we've seen what happens when we add records to the table. But, what happens when update or delete records, or even drop the entire table? These questions will have to wait for later posts. We hope that this post enlightened you a little bit to the purpose and structure of Azure Databricks Delta. Stay tuned for the next post where we'll dig a little deeper into the inner workings. Thanks for reading. We hope you found this informative.
Brad Llewellyn
Service Engineer - FastTrack for Azure
Microsoft
@BreakingBI
www.linkedin.com/in/bradllewellyn
llewellyn.wb@gmail.com

























